A weighted average is most often computed to equalize the frequency of the values in a data set. The survey team could weight the results of the 18-to-34 age group so that their views are represented proportionately. Then, consider this as the term and multiply that by $0.4$ when calculating the weighted average of the grade. A weighted average, on the other hand, is better when values have different amounts of worth or weight.

When Are Weighted Averages Used?
- This step gives you a series of products that represent the weighted contribution of each value.
- That is, the contribute a greater or a lesser amount to the final grade.
- A common mistake that can happen when working with big datasets is that values and their corresponding weights can get out of sync.
- An A in a five credit course would have a more significant impact on GPA than an A in a half-credit course.
The numbers that must be arranged refer to the grades you obtained in your quizzes, performance tasks, and final exam. A normal average calculation would completely miss this detail or require more data to provide the same accurate look. A normal average calculation would not be useful, as it would not account for these different volumes. Listed below are a few topics that are related to a weighted average. Weighted average are usually used for quantitative data, but can indeed lean over to the qualitative side or talk along it by taking numerical scores of qualitative categories.
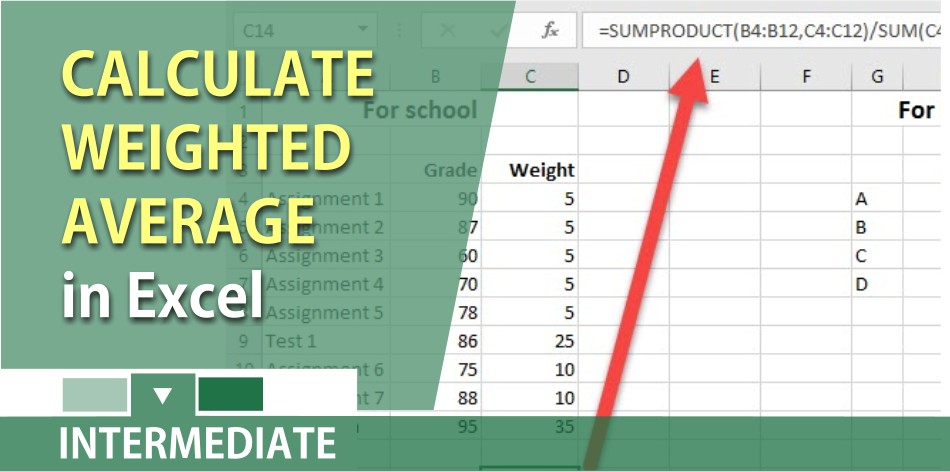
Method 2: When the Weights Do Not Add Up to One
Weight average also called weighted mean is helpful to make a decision when there are many factors to consider and evaluate. Each of the factors is assigned some weights based on their level of importance, and then the weighted average is calculated using a mathematical formula. The weighted average assigns certain weights to each of the individual quantities. The weights do not have any physical units and are only numbers expressed in percentages, decimals, or integers. The weighted average formula is the summation of the product of weights and quantities, divided by the summation of weights.
What is the difference between a weighted average and a simple average?
This formula represents the ratio of the sum of the products of each value (x) and its equal weight (w) to the sum of the weights. It’s just summing all scores and dividing the result by the total number of observations (4 courses). To figure out how to calculate a weighted average, we need to know the weight of each value. Typically, we present the weights in the form of a percentage or (in statistics) a probability of occurrence. Sometimes it may be a really significant difference – like a grade difference or even whether you pass or fail your course. For example, a teacher evaluates a student based on exam results, project work, attendance, and classroom behavior.
Example 2
If rounding in the middle is needed, keep the number of decimal places the same to cut down on rounding errors over time. When making key decisions, it’s best to double-check your calculations and keep a record of the original, unrounded numbers for future use. The student’s final grade averaged 89.5, reflecting the different weights of each educational component in the formula. Normally, when computing an average, each data point carries the same weight.
The weighted average method ensures that more significant numbers have a greater impact on the final average, making the weighted average a more accurate reflection of the data set. When some quantities are more important than the others and do not contribute equally to the final result thus multiplying them to a coefficient is called weighted average. It is a simple process of deriving at an average value between two or quantities when weight is added to it. For example, a student realizes that the scores after an exam is two times more important than the scores acquired during the quiz.
Weighted Average is a method of finding the average of a set of numbers where each number (or data point) is given a weight based on its importance or relevance. Weighted averages are commonly used in various fields such as finance, economics, education, and statistics, where different data points may have different levels of importance. This is the sum of the products of terms and their corresponding weights divided by the sum of the weights.
To find the weighted average, multiply each number by its own weight average, and then divide the sum of the results by the sum of the weights. All numbers are given equal consideration and weight when calculating a simple average, also known as an arithmetic mean. However, a weighted average applies weights that predetermine the proportional significance of each data point. These ratings could then be used as weights to calculate the weighted average score of different phone models.
Thirdly, weighted averages offer flexibility in their application across various fields and disciplines. Whether in finance, statistics, engineering, or manufacturing, weighted averages can be customized to suit specific needs and objectives. In a science class, labs are worth $50%$ of the grade, quizzes are worth $10%$ of the grade, homework is worth $15%$ of the grade, and tests are worth $25%$ of the grade.
In calculating a weighted average, each number in the data set is multiplied by a predetermined weight before the final calculation is made. The weighted average method is utilized in various journal entries for inventory transactions settings, including financial firms, statistical analysis, and classrooms. Instead of using the simple average alone, a user can better understand a set of facts by using a weighted average.
( b ) 10 weighted 25, 12 weighted 30, 16 weighted 20, and 15 weighted at 5. ( a ) 5 weighted at 20%, 7 weighted at 65%, and 8 weighted at 15%. ( a ) 5 weighted at 20%, 7 weighted at 65%, and 8 weighted at 15%.( b ) 10 weighted 25, 12 weighted 30, 16 weighted 20, and 15 weighted at 5. Weighted average calculations are used in many other jobs, such as by funding specialists and actuaries. This is true in situations such as calculating the benefits the average unemployed person receives.
0 Comments